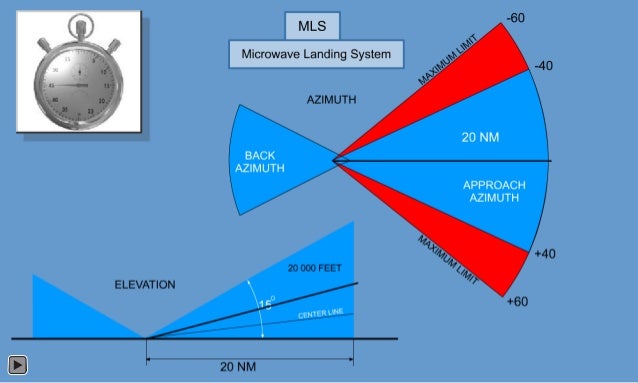
Azimuth And Elevation Pdf

A major component of a wireless LAN system is the antenna. There are several different types and they all have their place. However, there can be some confusion surrounding the language used to specify antennas as well as the basic function of each type of antenna. The purpose of this white paper is to dispel the confusion surrounding antennas and their function.

1. Dish Network Azimuth And Elevation
2. Azimuth And Elevation Pdf Online
3. Azimuth And Elevation Angle Calculation Pdf

This document is not meant to be an electromagnetic primer nor a deployment guide. Rather, it should be used as a dictionary of basic antennas and antenna terminology as well as a tutorial specifically covering antenna patterns and the parameters associated with those patterns. The focus is on many of the various antennas that might be encountered in a wireless LAN system.

We begin with a glossary of basic definitions and then progress through a discussion of some common antenna types and their properties. Along the way, the antenna patterns are shown and explained, including the 3-D radiation pattern from the antennas. Typical performance from each antenna type is described as well. Of course, there are plenty of exceptions to the 'typical' antenna, as many antenna types can be designed to enhance one or more parameters.

But it is often helpful to see a few examples and have some of these parameters highlighted. Antenna pattern. The radiation pattern orantenna pattern is the graphical representation of the radiation properties of the antenna as a function of space.

That is, the antenna's pattern describes how the antenna radiates energy out into space (or how it receives energy). It is important to state that an antenna radiates energy in all directions, at least to some extent, so the antenna pattern is actually three-dimensional. It is common, however, to describe this 3D pattern with two planar patterns, called theprincipal plane patterns. These principal plane patterns can be obtained by making two slices through the 3D pattern through the maximum value of the pattern or by direct measurement. It is these principal plane patterns that are commonly referred to as the antenna patterns.

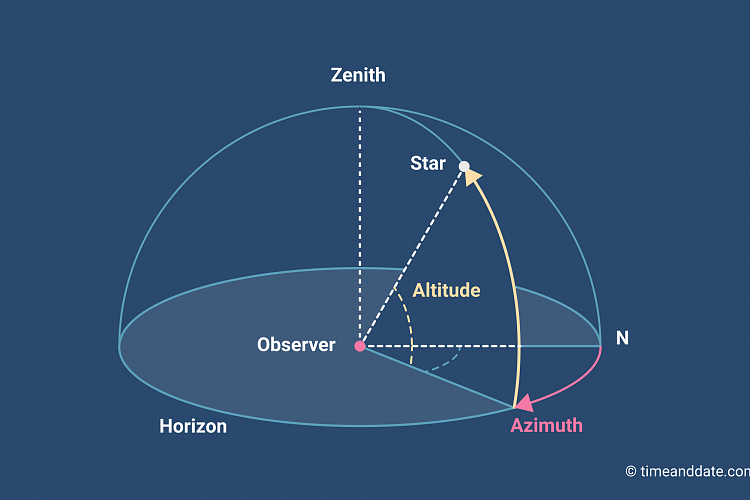
In discussions of principal plane patterns or even antenna patterns, you will frequently encounter the termsazimuth plane pattern andelevation plane pattern. The termazimuth is commonly found in reference to 'the horizon' or 'the horizontal' whereas the termelevation commonly refers to 'the vertical'. When used to describe antenna patterns, these terms assume that the antenna is mounted (or measured) in the orientation in which it will be used.

In Figure 2, the x-y plane (胃 = 90 deg) is the azimuth plane. The azimuth plane pattern is measured when the measurement is made traversing the entire x-y plane around the antenna under test. The elevation plane is then a plane orthogonal to the x-y plane, say the y-z plane (蠁 = 90 deg). The elevation plane pattern is made traversing the entire y-z plane around the antenna under test.

Any given antenna pattern has portions of the pattern that are calledlobes. A 'lobe' can be a main lobe, a side lobe or a back lobe and these descriptions refer to that portion of the pattern in which the lobe appears. In general, alobe is any part of the pattern that is surrounded by regions of relatively weaker radiation. So a lobe is any part of the pattern that 'sticks out' and the names of the various types of lobes are somewhat self-explanatory.

Figure 3 provides a view of a radiation pattern with the lobes labeled in each type of plot.Figure 3. Radiation Patterns in Polar and Cartesian Coordinates Showing Various Types of Lobes. Thegain of an antenna (in any given direction) is defined as the ratio of the power gain in a given direction to the power gain of a reference antenna in the same direction. It is standard practice to use an isotropic radiator as the reference antenna in this definition. Note that an isotropic radiator would be lossless and that it would radiate its energy equally in all directions.

That means that the gain of an isotropic radiator is G = 1 (or 0 dB). It is customary to use the unit dBi (decibels relative to an isotropic radiator) for gain with respect to an isotropic radiator.

Gain expressed in dBi is computed using the following formula. 3-dB beamwidth. The3-dB beamwidth (or half-power beamwidth) of an antenna is typically defined for each of the principal planes. The 3-dB beamwidth in each plane is defined as the angle between the points in the main lobe that are down from the maximum gain by 3 dB. This is illustrated in Figure 3.

The 3-dB beamwidth in the plot in this figure is shown as the angle between the two blue lines in the polar plot. In this example, the 3-dB beamwidth in this plane is about 37 degrees. Antennas with wide beamwidths typically have low gain and antennas with narrow beamwidths tend to have higher gain. Remember that gain is a measure of how much of the power is radiated in a given direction. So an antenna that directs most of its energy into a narrow beam (at least in one plane) will have a higher gain.

Thepolarization or polarization state of an antenna is a somewhat difficult and involved concept. An antenna will generate an electromagnetic wave that varies in time as it travels through space.

If a wave traveling 'outward' varies 'up and down' in time with the electric field always in one plane, that wave (or antenna) is said to belinearly polarized (vertically polarized since the variation is up and down rather than side to side). If that wave rotates or 'spins' in time as it travels through space, the wave (or antenna) is said to beelliptically polarized. As a special case, if that wave spins out in a circular path, the wave (or antenna) iscircularly polarized.

This implies that certain antennas are sensitive to particular types of electromagnetic waves. The practical implication of this concept is that antennas with the same polarization provide the best transmission/reception path. Consider antennas that generate and are sensitive to linearly polarized waves. If a linearly polarized antenna launches a linearly polarized electromagnetic wave traveling 'up and down' or vertically, the best possible receiver of that electromagnetic wave will be another antenna that is similarly linearly polarized (vertically polarized).

Linear polarization also includes the possibility of the electromagnetic waves traveling 'right to left' (horizontally) as well. Often antennas can simply be physically rotated to make them horizontally or vertically polarized, although this may not always be the best choice. Note that the polarization of an antenna doesn't always imply anything about the size or shape of the antenna. A dipole is usually called vertically polarized because of the way a dipole is typically used, that is, because it is mounted vertically, but the antenna is linearly polarized.

Likewise, antennas that are circular in their construction do not have to be circularly polarized. Many circular patches are linearly polarized and many rectangular patches are circularly polarized. These examples are simple demonstrations of the fact that the polarization state of an antenna is not related to its shape. Thevoltage standing wave ratio (VSWR) is defined as the ratio of the maximum voltage to the minimum voltage in a standing wave pattern. A standing wave is developed when power is reflected from a load. So the VSWR is a measure of how much power is delivered to a device as opposed to the amount of power that is reflected from the device.

If the source and load impedance are the same, the VSWR is 1:1; there is no reflected power. So the VSWR is also a measure of how closely the source and load impedance are matched. For most antennas in WLAN, it is a measure of how close the antenna is to a perfect 50 Ohms. It is important to mention that it doesn't really matter in which direction the patterns are shown. The orientation of a particular pattern is often a matter of personal preference. For example, some people like directional antenna patterns to always point up while others like them to point to the right or left because that's the way the antenna will often be deployed. The important thing is to have some basic knowledge of what these antennas are meant to do, so that you can understand the pattern parameters.

Then the pattern's direction is of little importance. Notice that the patterns in any orthogonal plane (any plane, actually) are directional in nature and so this antenna meets the definition of an omnidirectional antenna. The elevation plane pattern is formed by slicing the 3D pattern through an orthogonal plane (either the x-z plane or the y-z plane). From the elevation plane pattern we see that the dipole antenna has an elevation plane beamwidth of 78-degrees as indicated on the pattern in Figure 4d by the two blue lines. These lines are drawn where the gain is down from the peak by 3-dB.

The elevation plane beamwidth is the total angular width between the two 3-dB points on the curve. Given these antenna patterns, you can see that a dipole antenna should be mounted so that it is vertically oriented with respect to the floor or ground. This results in the maximum amount of energy radiating out into the intended coverage area. The null in the middle of the pattern will point up and down.

Indoors, this typically isn't a concern because of the close proximity of the ceiling and all the multipath present in the indoor environment.Figure 4. Dipole Antenna with 3D Radiation Pattern, Azimuth Plane Pattern and Elevation Plane Pattern. In order to create an omnidirectional antenna with higher gain, multiple omnidirectional structures (either wires or elements on a circuit board) can be arranged in a vertical, linear fashion to retain the same omnidirectional pattern in the azimuth plane but a more focused elevation plane beam which then has higher gain. This is frequently referred to as acollinear array. Note that the higher gain doesn't imply that the antenna creates more power.

It means that the same amount of power is radiated in a more focused way. A typical omni pattern is shown in Figure 5. The antenna shown in the figure was formed from an array of three dipoles, oriented along the z-axis. Notice now that the 3D pattern shown in Figure 5a looks like a flatter 'bagel' with a little 'bowl' stuck to the top and bottom. The bagel forms the omnidirectional azimuth plane shown in Figure 5b and the main lobes in the elevation plane, just like the dipole.

The little 'bowls' on the top and bottom form the sidelobes present in the elevation plane in Figure 5c. As is typical of higher gain omnidirectional antennas, the elevation plane shows obvious side lobes. The side lobes in the principal plane patterns are formed by slicing through the 'bowls' that sit above and below the main lobes in the 3D pattern. These lobes are about 14 dB down from the peak of the main lobes.

Note that the azimuth plane pattern is still the same well-behaved, circular pattern as in the dipole, but the elevation plane pattern is much narrower, indicating that the power is radiated in a more directed way, thus producing a higher gain.Figure 5. 3D Radiation Pattern from 5.8 dBi Omnidirectional Antenna, Azimuth Plane Pattern and Elevation Plane Pattern.

As shown in Figures 4 and 5, the goal of a dipole or any omni is to radiate energy equally in all directions in a plane. For dipoles and collinear arrays, the omnidirectional plane is intended to be the azimuth plane (the plane of the floor or the ground). For this reason, it doesn't matter how the patterns are presented. It is understood that the elevation plane pattern is always orthogonal to the azimuth plane pattern.

The orientation of the actual plot is largely dependent on the orientation of the antenna in the measurement system and that's all there is to it. So, whether the elevation plane looks like Figure 6a or Figure 6b, you can be certain that when your dipole or omni is oriented vertically, the antenna will radiate out toward the horizon in an omnidirectional fashion.Figure 6. Elevation Plane Demonstration. The patch antenna in Figure 7 shows how simple these antennas can be.

This is a simple rectangular patch built over a rectangular ground plane. The radiation patterns exhibit typical patch antenna characteristics. There is a single main lobe with a fairly wide beamwidth with shallow nulls pointing up and down from the antenna. Other than that, there aren't many features to the pattern. The one shown in Figure 7 is designed to have higher gain rather than symmetrical plane patterns. The gain is about 8.8 dBi with an azimuth plane beamwidth of 70 degrees and an elevation plane beamwidth of 57 degrees. These are not uncommon beamwidths for single patch antennas.Figure 7.

Single Patch Antenna with 3D Radiation Pattern, Azimuth Plane Pattern and Elevation Plane Pattern. The azimuth and elevation plane patterns are derived by simply slicing through the 3D radiation pattern. In this case, the azimuth plane pattern is obtained by slicing through the x-z plane, and the elevation plane pattern is formed by slicing through the y-z plane. Note that there is one main lobe that is radiated out from the front of the antenna. There are three back lobes in the elevation plane (in this case), the strongest of which happens to be 180 degrees behind the peak of the main lobe, establishing the front-to-back ratio at about 14 dB. That is, the gain of the antenna 180 degrees behind the peak is 14 dB lower than the peak gain. A patch array antenna is, in general, some arrangement of multiple patch antennas that are all driven by the same source.

Frequently, this arrangement consists of patches arranged in orderly rows and columns (a rectangular array) as shown in Figure 8. The reason for these types of arrangements is higher gain. Higher gain commonly implies a narrower beamwidth and that is, indeed, the case with patch arrays.

Illustrator text fonts. To quickly find fonts that you use frequently, you can perform the following actions in the Fonts tab of the Character panel or the Properties panel:.

The array shown here has a gain of about 18 dBi with an azimuth and elevation plane beamwidth of about 20 degrees. Notice that the back lobes are very small and that the front-to-back ratio is about 30 dB. The first sidelobes are down from the peak about 14 dB.Figure 8. A 4x4 Patch Array Antenna with 3D Radiation Pattern, Azimuth Plane Pattern and Elevation Plane Pattern. Antenna patterns are frequently shown normalized to the peak gain. The peak gain (in dBi) is simply subtracted from the gain at all the points on the curve and the pattern is plotted with the new values. These patterns are expressed in dB with 0 dB corresponding to the peak gain.

A normalized pattern is especially useful when the sidelobe levels and the depth of the nulls are of interest since it's easier to read their respective levels. The patterns of the patch array shown here have enough lobes and features that a look at their normalized patterns in rectangular coordinates might be interesting. Figure 9 shows the azimuth plane in both polar and Cartesian (rectangular) coordinates. Figure 10 shows the elevation plane in both coordinate systems. The side lobe levels are easily readable from the rectangular plots. In the azimuth plane, the side lobes are down about 14 dB from the peak.

The first side lobe levels are more than 14 dB down in the elevation plane. Note that the back lobe is 30 dB down from the peak. That means the front-to-back ratio is 30 dB.

Of course, if the patterns are given in normalized form, the peak gain must be given to determine absolute levels of any of the pattern parameters. The side lobes are labeled in all the plots.

Notice that the lower side lobes are to the left of the main beam in the Cartesian plots. These plots show the main beam at 0 degrees, so below the main beam would imply negative angle and above the main beam would imply positive angle.Figure 9.

Azimuth Plane Patterns of the 4 x 4 Patch Array in Polar and Rectangular Coordinates. A Yagi antenna is formed by driving a simple antenna, typically a dipole or dipole-like antenna, and shaping the beam using a well-chosen series of non-driven elements whose length and spacing are tightly controlled. The Yagi shown here in Figure 11 is built with one reflector (the bar behind the driven antenna) and 14 directors (the bars in front of the driven antenna). This configuration yields a gain of about 15 dBi with azimuth and elevation plane beamwidths that are basically the same, around 36 degrees.

That is a common feature of Yagi antennas. Many times these antennas are designed so that they can be rotated for either horizontal or vertical polarization, so having the same 3-dB beamwidth in each plane is a nice feature in those instances.Figure 11. Yagi Antenna Model with 3D Radiation Pattern, Azimuth Plane Patten, and Elevation Plane Pattern. A sector antenna or 'sector panel' is a somewhat specialized antenna frequently encountered in outdoor systems where wide coverage areas are desired. Very often they are built from an array of dipoles placed in front of a shaped reflector.

The size and shape of the reflector determines the performance of these antennas to a large extent. Many of these antennas have reflector shapes that are somewhat flat with some ridges or other features along the edges. A sector antenna is almost always categorized by its azimuth plane 3-dB beamwidth. Commonly available are 60-, 90-, and 120-degree sectors.

Sectors are frequently deployed higher up in the air and may have side lobe and front-to-back ratio requirements associated with them. The presence of other antennas and the height of the deployment can weigh heavily on the actual antenna selection. This is an 18 dBi, 90-degree sector. It is a 90-degree sector because the azimuth plane 3-dB beam is 90-degrees as shown in Figure 9e. In this case the elevation plane beamwidth is about 12 degrees and the first side lobes (elevation plane, Figure 9f) are down about 14 dB. Note that the principal plane patterns aren't oriented in any particular manner.

Remember that they don't really have to be oriented in any particular way when you know what the antenna is supposed to do. It is assumed that the azimuth plane is parallel to the ground and the elevation plane is perpendicular to the ground.Figure 12. Various 3D Radiation Patterns from a 90 degree Sector Antenna, Azimuth Plane Pattern and Elevation Plane Pattern.

One of the problems encountered when deploying sectors, or omnidirectional antennas for that matter, is that there can be several nulls in the elevation plane. When the gain is higher, the number of nulls (and side lobes) generally goes up as well. When the antennas are used in offices or in low hanging outdoor deployments, this is seldom a problem. Signal strengths are generally high enough everywhere to guarantee service to all users with careful planning.

But when the antennas are mounted high in the air on towers, these nulls can affect the performance of the system. Some sectors are specifically designed to combat this problem with 'null fill.' When the nulls are filled in, the distribution of energy to the various antenna elements in the array is changed so that more energy is radiated 'below' the antenna. As a result, the peak gain of the main lobe is generally reduced. In order to preserve the peak gain, more elements must be added and the antenna gets physically larger.

An example of a sector with 'null fill' is shown below in Figure 14. This is actually the Cisco® AIR-ANT2414S-R. The AIR-ANT2414S-R is a 14 dBi, 90-degree sector antenna. Many of the 90-degree sector antennas on the market for 2.4 GHz are shorter, but do not have the 'null fill' property. This antenna was designed to keep the gain relatively high while filling in the nulls 'under the antenna,' particularly the deep first null and second null that affect the coverage far away from the antenna.Figure 14. A Cisco 90-degree Sector Antenna with Azimuth and Elevation Plane Patterns. Notice that the first two nulls in the elevation plane 'under the antenna' are not as deep or seem to be gone altogether.

This allows for increased signal levels to users who might otherwise be without coverage as illustrated in Figure 15. The figure shows that if the antenna is tilted down 5 degrees as in the previously illustrated case, there is no null pointed far away from the antenna. The nulls that still exist point to areas close to the tower, where total lack of coverage is less likely due to the shorter ranges involved.Figure 15. Illustration of Reduced Coverage Gaps from a Sector Antenna with 'Null Fill'.

This paper covered basic antenna definitions and explained terms frequently encountered in examining antenna patterns. Gain and beamwidth definitions were made and pattern parameters such as front-to-back ratio and side lobe levels were discussed. Along the way, the basic function of several common antennas was covered. Omnidirectional antennas like dipoles and collinear arrays were shown to radiate their power out in all directions in a plane, away from the vertical axis of the antenna.

Increasing the gain reduces the elevation plane beamwidth and typically increases the number of side lobes. In general, directional antennas, like patches and Yagis, radiate their power out from the front of the antenna. In these cases, both the azimuth plane and elevation plane patterns become important. Increasing the gain will tend to reduce both the azimuth and elevation plane beamwidths unless specific design measures are taken. This is apparent in the design of sector antennas where the azimuth plane beamwidth is typically large compared to the elevation plane beamwidth. Finally, an illustration of some of the effects of nulls and side lobes was shown in the discussion of sector antennas.

Two sector antennas were shown mounted high on a tower. One of the sectors made no attempt to control the elevation plane nulls and the other was designed to fill in the worst of the nulls. The regions of low signal level resulting from elevation plane nulls were shown and discussed.

It is apparent from this simple discussion that antennas have to be carefully deployed to get the best performance from the system. Knowing the basic definitions and functionality of these common antenna types will provide the basis for good deployment decisions.References.

Polar-axis tracking is also called spinning-elevation tracking. The principle of the polar-axis tracking device is one axis of the collector or concentrator pointing to the celestial north pole, which is parallel to the earth's rotation axis.

The other axis is perpendicular to the polar axis, called the declination axis. When the device is working, the mirror or the collector rotates around the pole axis and the rotation speed is the same as that of the earth’s rotation angle, but the rotation direction is opposite. Fig. 5.12 shows the principle of a polar-axis tracking collector and Fig. 5.13 shows a polar-axis tracking heliostat in Shanxi Province, China; its total aperture is 16 m 2. Xianzheng Zhao.

Increase of radiation due to a rear reflector.A PV module (in green) with a tilt β = 25° receives the solar radiation which has an azimuth angle θ z = 30° (in this case radiation has an angle θ = 5° with the normal to the PV module). The solar rays are reflected by a flat aluminum module (in red) and the reflected rays increase the solar radiation on the PV module in the second row. In the drawing all the reflected radiation is uniformly distributed on the second module, so that, by geometrical consideration and neglecting losses due to the reflector efficiency, we can evaluate that the energy harvesting is increased by 42%.The calculation is based on the fact that the solar radiation G is captured with a negligible reduction factor of cos(30°– 25°) = 99.6% and that the reflected radiation is the one intercepted by the reflector 1.48-m long, that is 1.48sin(90 − γ − θ) = 0.74 and is spread over the full module 1.75-m long so that the increase is 0.74/1.75 = 42%. This is by far the best possible situation. However, several drawbacks are present: first of all the modules have to be oriented perpendicularly to the sunray direction so that a tracking system is necessary, but we also have to take into account the fact that for most of the time the reflected radiation does not hit the rear module uniformly, as is clearly shown in Fig. 2 where the reflection are analyzed for different times of day at the latitude of 37° 30′ (Catania, Italy) and with the parameters defined in Fig.

Radiation harvesting at Catania latitude for four different hours on August 20.In Fig. 2, it is quite evident that part of the reflected radiation is lost because not fully intercepted by the rear module (12 noon and 1 p.m.) and that at 2 p.m. The reflected radiation covers only part of the rear PV module.

The uneven distribution of irradiance on the PV modules, due to the reflectors, from the electrical point of view is similar to the shading phenomena described in Chapter 3: the bypass diodes would short circuit the part of the PV module where the irradiance has the lowest value. The possibility of changing the reflector or module tilt to get a uniform radiation it would solve this problem but, in our opinion, the resulting mechanical complexity is not acceptable.These problems are discussed in detail in several works: see Refs. The conclusion is that, when a tracking system is at work on the rear reflector, the energy harvesting can increase by a maximum of 20%, averaging the energy gain during the year. This is a nonnegligible gain but the requirement of a large space between module rows increases the raft cost. Experimental apparatus of a fixed low concentrating PV system at the DIEEI Department of the University of Catania (Catania, Italy).A test of this system has been done at Catania, without tracking and could be implemented on a floating power plant 2.In particular, the Catania group analyzes the gains (or losses) in term of annual harvesting of solar radiation for a fixed module + reflectors setup.

Dish Network Azimuth And Elevation

Furthermore, in order to solve the problem of the inhomogeneous radiation, the use of distributed maximum power point tracking (DMPPT) DC-DC converters is suggested. This could be a promising technique that allows the increase in efficiency and reliability of the whole system.Using this approach, the maximum power point tracking (MPPT) has been calculated for each group of cells within the string, and the resulting efficiency of the distributed architecture is higher than the one of the conventional typology where the MPPT is calculated in the centralized inverter. In this case efficiency increase with a fixed system can reach 25% at Catania latitude. Graph of the percentage variation of the monthly energy produced by a fixed low concentrating. PV system.As evident, large angles ( γ R = 20°–25°) give a 30%–40% increase in the energy harvesting during the summer months, which, due to the simplicity of the apparatus, is quite an interesting improvement.In the simulations, a constant PV cell temperature has been considered, which means that the results do not take into consideration the decrease of the PV module efficiency with the increase of the temperature. However, this hypothesis is applicable for FPV systems where the cooling by a water veil can be easily obtained.Moreover, it should be considered that the efficiency of a PV module depends on the angle of incidence of the solar irradiance.

The amount of solar radiation reaching the active surface, in fact, is affected by a number of optical effects related to collector geometry and material properties. The energy performance during the early and late hours of the day is greatly reduced due to large incidence angles. The same is for the reflected solar radiation, which shows large incidence angles during the mid-hours of the day, leading to great losses of performances.

The incidence angles depend on the tilt angle of the PV modules, β, and on the inclination angle of the reflectors, γ R. A possible solution could be the use of particular front glasses for PV modules. There are various suppliers of front glasses for PV modules on the market advertising the benefits of their products regarding optical transmittance and the angular characteristic. Outdoors, the textured front glasses and antireflection coating PV modules demonstrated higher specific energy yields also, leading to absolute energy gains of 3.0%–4.3% over the standard modules. While a significant gain was demonstrated, it was difficult to ascertain whether this was purely due to optical effects, as some suggestion of positive thermal and spectral effects was also found during data analysis 4. Figure 8.1.2.

Azimuth And Elevation Pdf Online

Two sensors and a point source.The signal energy corresponds to a wave propagating radially outward from the source location. If the physical size of the sensor array is very small compared to the distance between the source and sensor array (i.e., the source is in the far-field), the received wavefront may be considered as a plane across the array. Assuming the far-field scenario, the sources and array are coplanar, implying that the azimuth angle θ is the only relevant spatial parameter of a source. 8.1.2.1 Instantaneous mixing model. (8.1.5) x t = A s t + n ( t ),where x t = x 1 t, x 2 t, x m t T is the signal vector received at the M multiple sensors, vector s t = s 1 t, s 2 t, s n ( t ) T contains the source signals, and n( t) is an additive noise vector whose entries are modeled generally as stationary, temporally, and spatially white random processes, and independent of the source signals. The m × n matrix A represents the propagation matrix or mixing matrix, having n column vectors called steering vectors. The matrix A contains information on the DOAsof the different signals.

Equation ( 8.1.5) indicates that each sensor receives a contribution from each source resulting in the observations x i t i = 1 m. This mixture of n signals is shown in Fig. 8.1.4; the elements x i t i = 1 m of vector x t are linear superpositions of the source signals. In the simple case where the sensors receive signals from sources only through a single path (i.e., line-of-sight) and the observations x i t i = 1 m depend on the values of n source signals at the same time, such mixing process is referred to as instantaneous mixing.

Azimuth And Elevation Angle Calculation Pdf

The covariance matrix for Eq. ( 8.1.5) has the structure 4. The EEG measures the electrical activity produced by the nerve cells in the brain. The recordings are made using multiple electrodes placed on the scalp. Based on these multichannel EEG measurements (shown in Fig. 8.1.6), source localization can be performed to determine the location and strength of the contributing sources as well as their propagation path. The relationship between neural current sources and multichannel EEG measurements is governed by quasistatic approximations of Maxwell’s equations, which reduces to a Poisson equation as 5.

(8.1.10) ∇ ⋅ μ ∇ φ = ∇ ⋅ J s, in Ω,where ∇ is a partial differential vector operator, μ is the electrical conductivity, φ are the electrical potentials, and J s are the electric current sources. Equation ( 8.1.10) represents the distribution of the electric potential φ over the head volume Ω due to the primary current J s in the cortex of the human brain; it indicates that for a given configuration of electric sources, the mapping from electric sources within the head to the scalp recordings on the outside of the scalp can be represented by a lead-field matrix 6. The columns of the lead-field matrix represent the signal vectors that are observed at the scalp.Let us define x i t as the electric field measured at sensor i at time instant t.

The vector x t = x 1 t, x 2 t, x m ( t ) T is the set of measurements collected by m sensors. Let us assume n current dipole sources generate the electric field and b 1, b 2, b n represent the locations of these sources. The magnitude of the i th i = 1 n dipole source movement is s i t and the source magnitude vector is defined as s t = s 1 t, s 2 t, s n ( t ) T. For m sensors and n dipole sources, the relationship between x t and s t can be expressed by Eq.

( 8.1.5) using matrix A, which is a lead-field matrix of dimension m × n 6 that includes both the effect of location Λ and orientation Φ of the dipoles as A = Λ Φ. Each column of the lead-field matrix is called lead field and it defines the current flow for a given sensor through each dipole position 6.Hence, the array model can be used to solve the problem of EEG source localization.